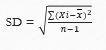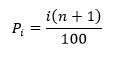DISTRIBUSI NORMAL DAN STANDAR DEVIASI

DISTRIBUSI NORMAL

Distribusi normal atau biasa di sebut distribusi gauss adalah salah satu distribusi peluang dengan variabel acak kontinu yang paling sering digunakan.

                     

Peran penting distribusi normal, yaitu:

·         Memiliki sifat yang dapat dijadikan satu patokan dalam pengambilan kesimpulan dari beberapa sampel

·         Distribusi normal terjadi secara alamiah, banyak peristiwa di dunia nyata yang terdistribusi secara normal

Fungsi kerapatan probabilitas dari distribusi normal diberikan dalam rumus berikut:

KURVA DISTRIBUSI NORMAL

Untuk menyelesaikan soal-soal peluang normal telah disediakan tabel nilai z.

Adapun cara untuk mencari nilai z adalah sebagai berikut:

MENENTUKAN LUAS DAERAH DENGAN MENGGUNAKAN TABEL Z

1.      Menghitung nilai Z sampai dua desimal.

2.      Menggambar kurva normal standar.

3.      Meletakkan nilai Z pada sumbu x kemudian menarik garis vertikal yang memotong kurva.

4.      Nilai yang terdapat dalam daftar merupakan luas daerah antar garis tersebut dengan garis vertikal di titik 0.

5.      Dalam daftar distribusi normal standar mencari tempat harga Z pada kolom paling kiri hanya sampai satu desimal dan mencari desimal kedua pada baris paling atas.

6.      Dari Z ke kolom kiri maju ke kanan dan dari Z di baris atau turun ke bawah, sehingga didapat bilangan yang merupakan luas daerah yang dicari.

Tabel Z score

UKURAN PENYEBARAN

Dispersi terdiri atas:

·         Jangkauan

·         Jangkauan antar Kuartil

·         Simpangan kuartil

1.      Jangkauan/Rentang

Jangkauan atau rentang atau range adalah ukuran dispersi yang paling mudah ditentukan.

J = Xmax - Xmin

Keterangan:

·         J = jangkauan/rentang/range

·         Xmax = nilai tertinggi dari data

·         Xmin = nilai terendah dari data

2.      Jangkauan antar Kuartil (JAK)/Hamparan (H)

Jangkauan antar kuartil atau biasa disebut hamparan merupakan selisih dari kuartil 3 dan kuartil 1.

3.      Simpangan Kuartil (Qd)

Simpangan kuartil atau jangkauan semi antar kuartil adalah setengah dari jangkauan antar kuartil.

STANDAR DEVIASI

Standar deviasi merupakan nilai statistika yang biasa digunakan untuk menentukan bagaimana sebaran data dalam sampel, serta beberapa dekat titik data individu ke mean atau rata-rata nilai sampel.

Fungsi Standar Deviasi

Standar deviasi umumnya dipakai oleh ahli statistik atau orang terjun di dunia statistik untuk mengetahui apakah sampel data yang diambil mewakili seluruh populasi. Mencari data yang tepat untuk suaatu populasi sangat sulit untuk dilakukan. Oleh karena itu dipakai sampel data yang mewakili seluruh populasi. Hal ini akan memudahkan seseorang untuk melakukan penelitian.

Rumus

·         Data tunggal

n > 30

n ≤ 30

·         Data kelompok

n > 30

n ≤ 30

       

KUARTIL, DESIL DAN PERSENTIL

I.                   Kuartil

Kuartil adalah kumpulan data yang sudah diurutkan dari data terkecil hingga data terbesar atau sebaliknya yang kemudian dibagi menjadi empat bagian yang sama banyak.

Kuartil dibagi menjadi tiga macam yaitu K₁, K₂, K_3. Pemberian nama ini ditentukan dari nilai kuartil yang paling kecil. (Andi, 2007)

A.    Kuartil Data Tunggal

1.      Menyusun data dimulai dara data terkecil hingga data terbesar

2.      Menentukan letak kuartil yang diminta dengan menggunakan rumus

K_i = kuartil ke-

n = jumlah data

i = letak kuartil

contoh soal

berikut adalah nilai statistika semester 2 dari 10 mahasiswa: 60, 80, 90, 70, 85, 95, 75, 65, 50, 55. Tentukanlah nilai K₂.

1.      Mengurutkan data dari yang terkecil ke terbesar: 50, 55, 60, 65, 70, 75, 80, 85, 90, 95

2.      Menentukan K₂

Dari data tersebut maka data ke 5,5 berada di antara data ke-5 dan ke-6, jadi

K₂ = data ke-5 + 0,5 (data ke-6 – data ke-5)

K₂ = 70 + 0,5 (75 – 70)

K₂ = 70 + 0,5 (5)

K₂ = 70 + 2,5

K₂ = 72,5

Jadi, nilai dari kuartil 2 adalah 72,5.

B.     Kuartil Data Kelompok

b = tepi bawah kelas interval kelas K_i (b = batas bawah – 0,5)

p = panjang kelas interval

i = letak K_i

n = banyak data

Fk = frekuensi kumulatif sebelum kelas K_i

f = frekuensi pada kelas K_i

II.                Desil

Desil adalah nilai atau angka yang membagi data menjadi 100 bagian yang sama setelah disusun dari data terkecil hingga data terbesar atau sebaliknya. Desil hanyak memiliki 9 nilai.

Ada dua kelompok desil yaitu nilai data desil yang belum dikelompokkan (data tunggal) dan nilai data desil yang sudah dikelompokkan (data berkelompok).

A.    Desil Data Tunggal

D_i = desil ke-

n = jumlah data

i = urutan desil

contoh soal

nilai statistik 10 mahasiswa: 60, 80, 90, 70, 85, 95, 75, 65, 70, 65. Tentukanlah nilai D₇.

1.      Mengurutkan data: 60, 65, 65, 70, 70, 75, 80, 85, 90, 95.

2.      Masukkan data ke rumus utama:

D₇ = data ke-7 + 0,7 (data ke-8 – data ke-7)

D₇ = 80 + 0,7 (85 – 80)

D₇ = 80 + 0,7 (5)

D₇ = 80 + 3,5

D₇ = 83,5

Jadi, nilai desil 7 adalah 83,5.

B.     Desil Data Berkelompok

b = tepi bawah kelas interval

p = panjang kelas interval

i = letak Ds_i

n = banyak data

Fk = frekuensi kumulatif sebelum kelas Ds_i

f = frekuensi kelas Ds_i

III.             Persentil

Persentil adalah nilai yang membagi data menjadi 100 bagian yang sama. Setelah disusun dari angka terkecil sampai ke yang terbesar. Harga persentil ada 99 bagian yaitu Ps₁, Ps₂, Ps₃, ..., Ps₉₉.

A.    Persentil Data Tunggal

P_i = persentil ke-

n = jumlah data

i = urutan persentil

contoh soal

data tunggal terdiri dari 35, 47, 58, 67, 83, 87, 89, 90, 91, 95. Tentukanlah persentil ke-80.

P₈₀ = data ke-8 + 0,8 (data ke-9 – data ke-8)

P₈₀ = 90 + 0,8 (91 – 90)

P₈₀ = 90 + 0,8 (1)

P₈₀ = 90 + 0,8

P₈₀ = 90,8

Jadi, nilai dari persentil ke-80 adalah 90,8.

B.     Persentil Data Berkelompok

b = tepi bawah kelas interval

p = panjang kelas interval

i = letak Ps_i

n = banyak data

Fk = frekuensi kumulatif sebelum kelas Ps_i

f = frekuensi kelas Ps_i